计算智能导论
计算智能导论
前言:
首先,这是自用的复习资料,发出来如果未来被本校学弟学妹看见了那是属实荣幸;其次,这本书本身就是有不少问题的,如果在我的文档里发现了bug不要惊慌,属于正常操作,有能力的话还请更改了之后push到Github并在最后留下你的足迹;最后,这只是一个零基础学渣在考前一周的复习,内容完全按照考点来设置,建议给人预习留个念想啥的,以及给摆烂人最后突击用的。
修改于2022/7/1,已经考完试了,现在的版本是在原有基础上对整个文档进行的一个补充完善,通过从考试的试卷来阐述只需要完善的复习要点,所有内容都放在第4章之后的2.0补充内容中。
第1章 绪论——从人工智能到计算智能
1、计算智能定义(P11)
计算智能系统是在神经网络、模糊系统、进化计算三个分支发展相对成熟的基础上,通过相互之间的有机融合而形成的新的科学方法,也是智能理论和技术发展的崭新阶段。当一个系统仅仅处理底层数据,具有模式识别的部分,并且不使用AI意义中的知识,那么这个系统就是计算智能系统。
2、人工神经网络的特点(P10)
(1)信息的分布表示记忆在大量神经元中。每个神经元存储许多信息的部分内容,信息在神经网络中的记忆反映在神经元间突触的连接强度上。
(2)神经网络运算的全局并行和局部操作。神经网络具有高度的并行结构和并行实现能力,因而有较好的耐故障能力和较快的总体处理能力。
(3)处理的非线性。神经网络具有非线性特性,这源于其近似任何非线性映射(变换)的能力。
(4)较强的学习能力。神经网络是通过研究系统过去的数据记录进行训练的。一个经过适当训练的神经系统具有归纳全部数据,因此,神经网络能够解决那些由数学模型或描述规则难以处理的控制过程的问题。
第2章 进化算法
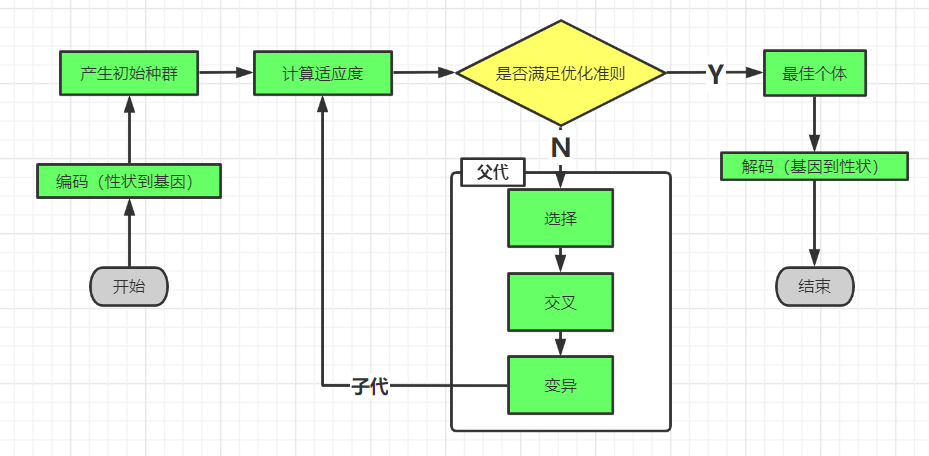
1、遗传算法的基本框架(P40)
2、遗传算法的优点(P40)
(1)遗传算法直接以目标函数值作为搜索信息。传统的优化算法往往不只需要目标函数值,还需要目标函数的导数等其他信息,这样对于许多函数无法求导或很难求导的函数,遗传算法就比较方便。
(2)遗传算法同时进行解空间的多点搜索。传统的优化算法往往从解空间的一个初始节点开始搜索,这样容易陷入局部极值点。遗传算法进行群体搜索,并且在搜索的过程中引入遗传运算,使群体又可以不断进化,这些是遗传算法所特有的一种隐含并行性,因此,遗传算法更适合大规模复杂问题的优化。
(3)遗传算法使用概率搜索技术。遗传算法属于一种自适应概率搜索技术,其选择、交叉、变异等运算都是以一种概率的方式来进行的,从而增加了其搜索过程的灵活性。实践和理论都已证明,在一定条件下遗传算法总是以概率1收敛于问题的最优解。
(4)遗传算法在解空间进行高效启发式搜索,而非盲目地穷举或完全随机搜索。
(5)遗传算法计算简单、功能强。
3、遗传算法的五个关键问题(P41)
(1)对问题的潜在解进行基因的表示,即编码问题。
(2)构建一组潜在的解决方案,即种群初始化问题。
(3)根据潜在解的适应性来评价解的好坏,即个体评价问题。
(4)改变后代基因组成的遗传算子(选择、交叉、变异等),即遗传算子问题。
(5)设置遗传算法所用的参数值(种群大小、应用遗传算子的概率等),即参数选择问题。
4、遗传编码(P41)
定义
由问题空间向GA编码空间的映射称为编码,而由编码空间向问题空间的映射称为译码。
1、编码的分类
(1)根据采用的符号,编码可以分为二进制编码、实数编码和整数排列编码等。
(2)根据编码采用的结构,编码可以分为一维编码和多维编码。
(3)根据编码采用的长度,编码可分为固定长度编码和可变长度编码。
(4)根据编码的内容,编码可分为仅对解进行编码的方法和对解+参数进行编码的方法.
2、码空间和解空间
遗传算法的一个特点就是个体存在于码空间和解空间:遗传操作在码空间,而评价和选择在解空间,通过自然选择将染色体和解连接起来。
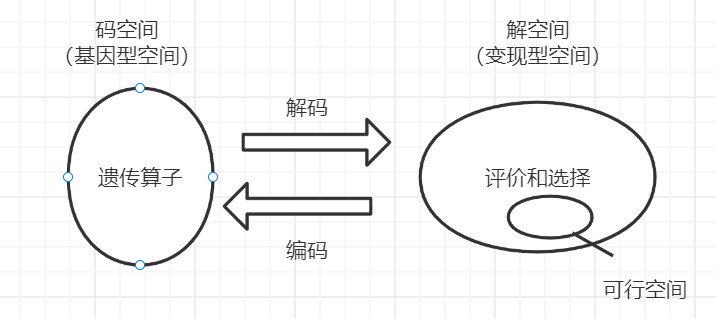
3、非字符编码的三个问题
(1)染色体的可行性,是指染色体经过解码之后,是否存在于给定问题的可行域。
(2)染色体的合法性,编码空间中的染色体必须对应问题空间中的某一潜在解,即每个编码必须有意义。
(3)映射的唯一性,染色体和潜在解必须一一对应。
4、编码性能评价
码空间到解空间有以下三种情况:1对1映射、n对1映射和1对n映射。
1对1映射是三种映射中最好的;1对n映射是三种映射中最差的,存在适应度评价问题;n对1映射则会存在资源的浪费。
(1)不冗余:码空间到解空间是1对1映射;
(2)合法性:对编码的任意排列对应一个解;
(3)完备性:任意一个解都对应一个排列。
5、适应度函数(P54)
遗传算法在进化搜索中基本不用外部信息,仅以目标函数即适应度函数为依据,利用种群每个个体的适应度来指导搜索。遗传算法的目标函数不受连续可微的约束,且定义域可以为任意集合。
适应度函数值是选择操作的依据,适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优解。
第3章 模糊逻辑
1、概率与模糊(P165)
相似之处
(1)都可以用来刻画不确定性。
(2)都通过单位间隔【0,1】中的数来表述不确定性,即映射的值域是相同的,均为【0,1】。
(3)都兼有集合和命题的结合律、交换律、分配律。
区别
$$
(1)经典集合论中A\cap A^C = \varnothing,P(A\cap A^C) = P(\varnothing) = 0代表概率上不可能的事件;模糊集合建立在A\cap A^C = \varnothing的基础上。
$$
(2)经典集合A中某个元素x的概率在x发生之后,就会变为0或1;模糊集合A中某个元素x的隶属度不会发生变化。
(3)概率是事件是否发生的不确定性;模糊是事件发生的程度。
2、模糊集合的表示方法(P170)
列举法
只适用于有限集合。当论域U是离散域时,一般可以用扎德(Zadeh)表示法、序偶表示法和向量表示法表示。这三种方法均属于列举法。
(具体三者的公式见书P170)
描述法
对于无限集,可以使用描述法表示集合,即
$$
A = {x | P(x) }
$$
其中,P(x)表示x满足性质P。
隶属度函数法(重点)
论域E上的模糊集合A是由隶属度函数确定的,所以可以用隶属度函数来表示模糊集合A。模糊集合可表示为:
$$
\mu(x) =
\begin{cases}
1, 当x\in A \
0 < \mu_A(x) < 1,当A在一定程度上属于A时 \
0, 当x\notin A
\end{cases}
$$
3、模糊集合的几何图示(P172)
详细见书P172。
4、模糊集合的基本运算(P174)
(1)相关运算的定义
$$
相等: A = B \Leftrightarrow \mu_A(x) = \mu_B(x) \
包含: A \subseteq B \Leftrightarrow \mu_A(x) \leq \mu_B(x) \
交集: C = A \cap B \Leftrightarrow \mu_A(x) = min(\mu_A(x), \mu_B(x)) = \mu_A(x) \land \mu_A(x) \
其中,“\land”为Zadeh算子,表示“取最小值”运算 \
并集: C = A \cup B \Leftrightarrow \mu_A(x) = max(\mu_A(x), \mu_B(x)) = \mu_A(x) \lor \mu_B(x) \
其中,“\lor”为Zadeh算子,表示“最大”运算 \
补集: \overline{A} \Leftrightarrow \mu_\overline{A}(x) = 1 - \mu_A(x) \
代数集: 模糊集的代数集,记为AB,其隶属度函数定义为 \mu_{AB} = \mu_A \mu_B \
代数和:模糊集A、B的代数和,记为A⊕B,其隶属度函数定义为 \mu_{A⊕B} = \mu_A + \mu_B - \mu_{AB} \
绝对差:模糊集A、B的代数差,以|A - B|表示,其隶属度函数定义为\mu_{|A-B|} = \mu_A - \mu_B
$$
(2)基本定律
$$
幂等律: A \cap A = A \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cup A = A \
结合律:A \cap (B \cap C) = (A \cap B) \cap C \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cup (B \cup C) = (A \cup B) \cup C \
交换律:A \cap B = B \cap A \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cup B = B \cup A \
分配律:A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \
同一律:A \cap U = A \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cup \varnothing = A \
零一律:A \cup U = U \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cap \varnothing = \varnothing \
吸收律:A \cap (A \cup B) = A \
\ \ \ \ \ \ \ \ \ \ \ \ \ A \cup (A \cap B) = A \
德-摩根律:\overline{A \cap B} = \overline{A} \cup \overline{B} \
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \overline{A \cup B} = \overline{A} \cap \overline{B} \
双重否定率:\overline{\overline A} = A
$$
(3)一些常用的算子
$$
\begin{aligned}
Zadeh算子(\land,\lor):& a \lor b = max{a,b} \
& a \land b = min{a,b} \
取大、乘积算子(\lor,\cdot): & a \lor b = max{a,b} \
& a \cdot b = ab \
环和、乘积算子(⨣,):& a ⨣ b = a + b - ab \
& a \cdot b = ab \
有界和、取小算子(⊕,\land):& a ⊕ b = 1 \land (a + b) \
& a \land b = min{a, b} \
有界和、乘积算子(⊕,\cdot):& a ⊕ b = 1 \land (a + b) \
& a \cdot b = ab \
Einsain算子(ε^+,ε^-):& a ε^+ b = \frac{a + b}{1 + ab} \
& a ε^- b = \frac{ab}{1 + (1-a)(1 - b)}
\end{aligned}
$$
5、隶属度函数定义(P178)
论域U上的一个模糊集A由隶属函数μA(x)唯一确定,表示x隶属于集合A的程度,故认为二者是等同的,即
$$
\mu_A: U \longrightarrow[0,1]
$$
6、α水平载集的定义和计算(P189)
α水平载集是指隶属度大于等于α的元素组成的集合,可表示为
$$
A_\alpha = { x | \mu_A(x)}
$$
注意:模糊子集本身没有确定边界,其水平载集有确定边界,并且不再是模糊集合,而是一个确定集合。
7、模糊集合(P194)
(1)如果关系R是XxY的一个模糊子集,则称R为XxY的一个模糊关系,其隶属度函数为μR(x,y)。
注意:隶属度函数μR(x,y)表示x、y具有R的程度。
(2)若一个矩阵元素取值在【0,1】区间内,则称该矩阵为模糊矩阵。同普通矩阵一样,模糊单位阵记为I;模糊零矩阵记为0。
(3)模糊矩阵的表示。当X和Y都是有限集合时,模糊关系也可以用MR来表示。设X = { x1 , x2 , … , xi , …xn },Y = { y1 , y2 , … , yi , …yn },则MR可以表示为
$$
M_R = [r_{ij}]{m \times n} , r{ij} = \mu_R(x_i,y_i)
$$
(关于3,建议大家还是看一下书本P194的例题来快速理解,当然这个例题是有错误的,需要大家自己甄别了)
8、极大运算(P196)
(1)极大-极小复合运算
设R1和R2分别是定义在XxY和YxZ上的两个模糊关系,R1和R2的极大-极小复合运算可得到一个模糊关系(集合),可表示为
$$
R_1 ○ R_2 = { [(x , z), \max \limits_{y} \min [\mu_{R_1}(x,y),\mu_{R_2}(y,z)]] }
$$
(2)极大-乘积复合运算
设R1和R2分别是定义在XxY和YxZ上的两个模糊关系,R1和R2的极大-乘积复合运算可得到一个模糊关系(集合),可表示为
$$
R_1 ○ R_2 = { [(x , z), \max \limits_{y}[\mu_{R_1}(x,y) \times \mu_{R_2}(y,z)]] }
$$
关于两个的实际运算见书P197,太多了题主懒得打,其实很好理解,拿极大-极小复合运算举例,极大在前面,那么极大就把极小运算包裹,先做一个极小的矩阵运算后对结果矩阵进行一个极大运算。
第4章 人工神经网络
1、生物神经系统的特点(P261)
(1)生物神经元之间相互连接,其连接强度决定了信号传递的强弱;
(2)神经元之间的连接强度是可以随着训练改变的;
(3)信号可以起刺激作用,也可以起抑制作用;
(4)一个神经元接收信号的累积效果决定了该神经元的状态;
(5)每一个神经元有一个动作阈值。
2、激活函数(P263)
激活函数模拟的是生物神经元对输入信息的处理。激活函数对输入感知器的信息进行处理,并决定其是否有对应的输出以及输出幅度有多大,也可以称为激励函数、活化函数、传递函数等,表达式为
$$
y = \varphi(u + b)
$$
其中φ(*)表示激活函数。激活函数是感知器处理的核心部分,引入激活函数增加了神经网络的非线性特性,从而使得神经网络能够实现各种复杂功能。如果没有激活函数,无论叠加多少层神经网络,起计算过程都只是线性计算,结果也是个普通矩阵而失去了强大的映射能力。激活函数在神经网络中的地位可见一斑。常见的激活函数:
(1)硬极限传输函数
$$
f(n) =
\begin{cases}
\beta, n \geq \theta \
- \gamma , n < \theta
\end{cases}
$$
其中,β、γ、θ均为非负实数,θ为阈值。当β=1、γ=0时,函数表现为二值形式;当β=1、γ=1时,函数表示为双极形式。
(2)线性传输函数
$$
f(n) = w^Tp + b
$$
当b = 0时,传输函数关于原点中心对称,这是常见的一种形式。
(3)对数S型函数
对数S型函数的两种形式分别为逻辑斯特函数和压缩函数。
【1】逻辑斯特函数(Logistic Function)
$$
f(n) = \frac{1}{1 + e^{-d \times n}}
$$
其中,d为常实数,函数的饱和值为0和1。
【2】压缩函数(Squashing Function)
$$
f(n) = \frac{g + h}{1 + e^{-d \times n}}
$$
其中,g、h、d为常数,函数的饱和值为g和g+h。
(4)其他常见传输函数
【1】硬极限函数(Hardlim)
$$
f =
\begin{cases}
0, n < 0 \
1, n \geq 0
\end{cases}
$$
【2】对称极限函数(Hardlims)
$$
f =
\begin{cases}
-1, n < 0 \
1, n \geq 0
\end{cases}
$$
【3】线性函数(Pureline)
$$
f = n
$$
【4】饱和线性函数(Satlin)
$$
f =
\begin{cases}
0, n < 0 \
n, 0 \leq n \leq 1 \
1, n > 1
\end{cases}
$$
【5】对称饱和线性函数(Satlins)
$$
f = \frac{1}{1 + e^{-n}}
$$
【6】双曲正切S型函数(Tansigs)
$$
f = \frac{e^n - e^{-n}}{e^n + e^{-n}}
$$
【7】正线性函数(Poslin)
$$
f =
\begin{cases}
0, n < 0 \
n, n \geq 0
\end{cases}
$$
3、离散单输出感知机训练算法(P268)
训练样本集为{(X,Y)| Y },其中Y为输入向量X对应的输出。权向量W = (ω1,ω2,…,ωn),其中n为输入向量的维数。输入向量X = (x1,x2,…,xn ),其中n为输入向量的维数。输出向量O=(0,1)。激活函数为f。
算法的具体流程
(1)随机初始化权向量W;
(2)对每个样本(X,Y),计算O = f(XW),对i∈[ 1 , n ],n为样本数,执行下式:
$$
W_i =
\begin{cases}
W_i + X_i, O < Y \
W_i - X_i, O > Y
\end{cases}
$$
(3)重复第(2)项,直到训练完成。
4、梯度下降方法(P276)
梯度下降方法是最常见的训练神经网络参数的方法之一。
1、损失函数
在机器学习中每个算法都会有一个目标函数,而算法的运行求解过程通常也就是这个算法的优化求解过程。在一些算法求解问题中,常会使用损失函数作为目标函数。损失函数代表的是预测值和真实值之间的差异程度,那么只要找到一个解使得二者之间的差异最小,该解就可以理解为此时的一个最优解。通常损失函数越好,则模型的性能也越好。常见的损失函数有如下几种:
【1】0 - 1损失函数(0 - 1 Loss Function):
$$
L(Y, f(x)) =
\begin{cases}
1, Y \neq f(x) \
0, Y = f(x)
\end{cases}
$$
【2】平方损失函数(Quadratic Loss Function):
$$
L(Y, f(x)) = (Y - f(x)) ^ 2
$$
【3】绝对损失函数(Absolute Loss Function):
$$
L(Y, f(x)) = ||Y - f(x)||
$$
【4】对数损失函数(Logarithmic Loss Function)或对数似然损失函数(Log-Likelihood Loss Function):
$$
L(Y, P(Y|X)) = -\lg P(Y|X)
$$
2、梯度的理解
在多元函数中对各个参数求偏导,最后把各个参数的偏导数用向量的方式表示出来即梯度。从二维到三维函数的图像中可知,梯度可以代表函数在这个参数上的变化速度快慢,梯度越大则变化越快。沿着梯度变换的方向直至梯度为0,该处通常是一个局部的高点或者低点,即极大值或者极小值,在函数中这恰恰可以视为函数的最终解。
在人工神经网络的训练中,需要最小化损失函数时,可以通过梯度下降方法来进行多次迭代求得最优解。在函数图像上,最低点就是最小化的损失函数结果。同理,如果要求解梯度的最大值,则可以采用梯度上升的方式得到一个梯度最大值,其对应的是损失函数的极大值。两者之间也可以互相转换,例如原本是求损失函数的极大值,经过取反可以变为求解一个损失函数的极小值。另外,这种求解方法求得的解是局部极大或极小值,但不一定是全局最大或最小值。
3、梯度下降的学习规则
学习率 X 负梯度
4、梯度下降方法的实现
(1)确定优化模型的假设函数和损失函数。以线性回归为例,假设函数如下:
$$
h_\theta(x_1, x_2, \cdots, x_n) = \theta_0 + \theta_1x_1 + \cdots + \theta_xx_n
$$
其中,θi(i = 0,1,2,…,θn)为模型参数,xi(i = 0,1,2,…,n )为每个样本的n个特征值。θ0可以看作θ0x0(x0=1),故
$$
h_\theta(x_1, x_2, \cdots, x_n) = \sum_{i=0}^n \theta_ix_i
$$
对应的损失函数为
$$
J(x_1, x_2, \cdots, x_n) = \frac{1}{2m} \sum_{j=0}^m (h_\theta (x_0^j, x_1^j, \cdots, x_n^j) - y_j)^2
$$
(2)初始化参数:θi(i = 0,1,2,…,θn)、算法终止误差为ε、梯度下降步长为α。θ可以随机生成,步长初始化为1;ε根据需要的精确度来设置,ε越小可能算法运行时间就越长。后续可以根据运行结果再调整参数。
(3)算法过程如下:
【1】求梯度:
$$
\nabla_i = \alpha \frac{\partial}{\partial \theta}J(\theta_0, \theta_1,\cdots, \theta_n)
$$
【2】若|∇i| < ε,则运行结束,输出θi(i= 0,1,2,…,n);若|∇i| >= ε,则运行下一步;
【3】更新所有的θ:
$$
\theta_i = \theta_i - \alpha \frac{\partial}{\partial \theta}J(\theta_0, \theta_1,\cdots, \theta_n)
$$
更新完,转步骤【1】。(重点公式)
【4】加快收敛的方法:
- 特征缩放。在多特征问题中保证特征有相近的尺度将有利于梯度下降。
- 通过调整学习率来更改收敛速度。学习率过小会导致梯度下降方法收敛过慢,但过大也可能使得网络不能收敛。
【5】多种梯度下降方法:
- 批量梯度下降方法(Batch Gradient Descent)
这是梯度下降方法中使用最多的形式之一,其具体操作是在更新参数时,使用所有的样本来进行更新。缺点在于由于训练的样本大,训练速度会变慢。
- 随机梯度下降方法(Stochastic Grandient Descent)
该方法和批量梯度下降方法原理类似,区别在于求梯度时没有采用所有的样本数据,而仅仅选取一个样本求解梯度。其优点在于只采用一个样本迭代,故训练速度极快;缺点在于迭代方向变化很大,不过很快收敛到局部最优解。
- 小批量梯度下降方法(Mini-batch Gradient Descent)
该方法综合了上述两种方式的优缺点,即对于m个样本,就采用x个样本来迭代,1<x<m,可以根据样本数据调整x的值。
5、误差反向传播算法(P280最后一个大题)
原理(选择题)
在消息正向传播的过程中,信息经过输入层到达隐含层,再经过多个隐含层的处理后到达输出层;比较输出结果和正确结果,将误差作为一个目标函数进行反向传播,对每一层依次求神经元权值的偏导数,构成目标函数对权值的梯度,网络权重再依次完成更新调整。依此往复,直到输出达到目标值完成训练。
总结
利用输出误差推算前一层的误差,再用推算误差算出更前一层的误差,直到计算出所有层的误差估计。
前向传播
前向传播简而言之就是从输入层开始,信号输入神经元,经过加权偏置激活函数的处理输出,称为下一级的输入参数,如此往复直到从输出层输出。
主要公式
$$
z^l = W^la^{l-1} + b^l \
a^l = f(z^l)
$$
反向传播
反向传播以前向传播为基础,从前向传播得到的参数前反向推导更新每一层的权重和偏置。
假定以误差平方作为损失函数,将该目标函数作为优化目标:
$$
J (W, b) = \frac{1}{2} \sum_{j = 1}^l (\hat y_i - y_i) ^2
$$
其中,两个yi分别表示神经网络的输出结果和数据集给出的真实结果。
根据梯度下降方法的原理,可以按照如下方式更新参数:
$$
W^l = W^l - \alpha \frac{\partial J (W, b)}{\partial W ^ l} \ \ \ \ \ (权值调整)
$$
2.0补充
该部分内容为考试结束后进行实况整理分为选择题、填空题、大题三个部分(简答题并不固定,也一并放在大题之间)。
选择题
选择题主要以背记部分为主,字面意义上的背记部分,比如遗传算法的特点、生物神经算法的特点等内容,也就是说在简答题自己对简答题的背记能够完全应付考试中的选择题部分。
填空题
填空题部分需要大家多对老师上课的知识内容进行留意(特指老师讲过5遍以上的内容),这次的填空题5空10分,后三空是一个简单的大题(参考P189 α水平载集例题改编),第一二空为:
- 老师上课常说的“假小明”指的是什么?(A:我写的是不同的输入,但是不确定答案的正确性)
- 老师上课最常说的七字学习规则是什么?(A:学习率x负梯度)
大题
大题出的中规中矩,其余不做过多说明,最后一个大题可以参考用例:
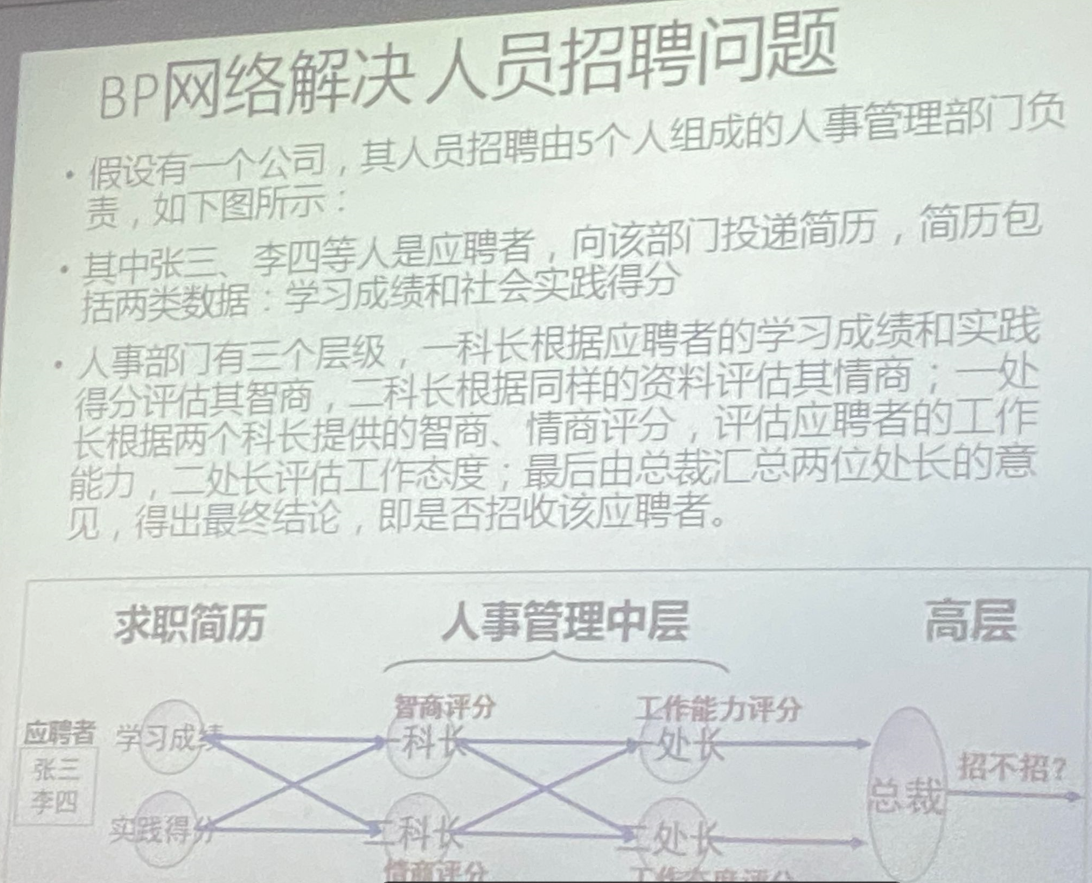
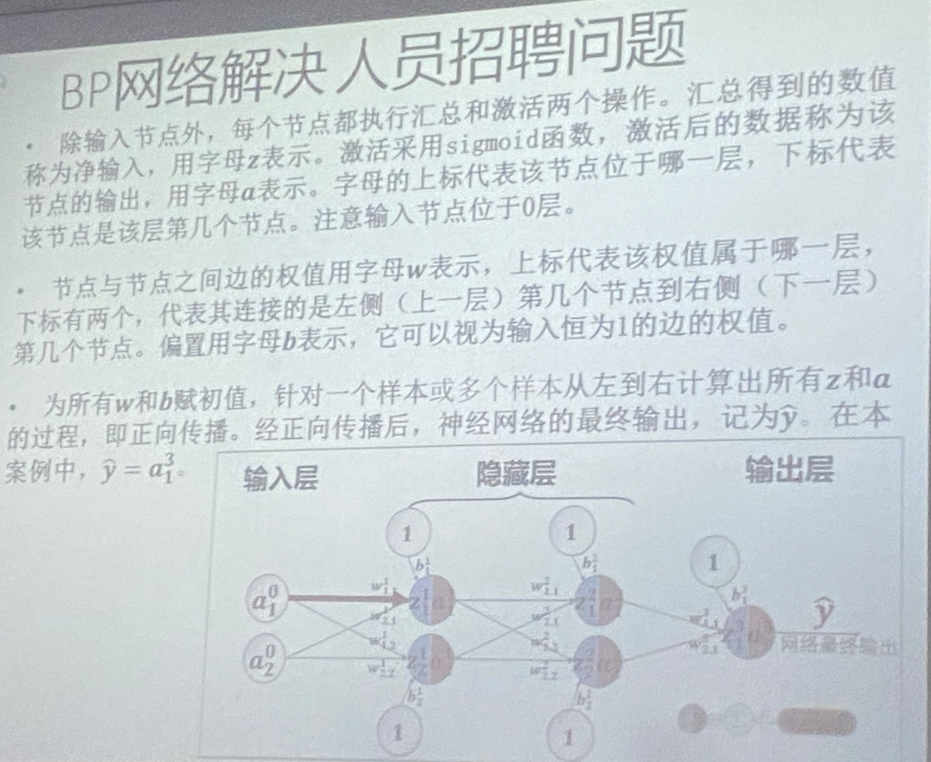
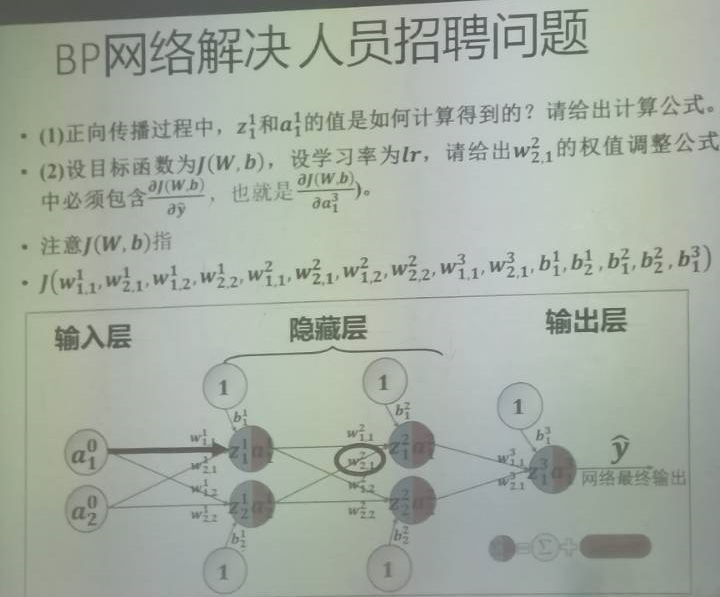
总结
这个文档到这里就告一段落了,东西不算多,但也决说不上少了,可以看出整个科目便向数学计算和理论算法,所以真正想学好的话还是需要个人去把(丢掉的)数学学好吧。这个文档不适合作为学科学习,但可以作为入门参考资料,应付考试的理论部分看这个文档基本上是够用了,但是解题部分我更建议大家去看看书上的例题,就像我标记了重点的那几页的例题必须是需要自己去看去了解的。
因为例题太难敲了所以我就没放到文档里,不然真成应试文档了(😀),希望有机会看到这个文档的还是需要花时间去啃下这些硬骨头,后续还会慢慢出学习文档的。但是也会有出着出着自己学会了就不想出的(比如说《人工智能导论》)。最后希望能够帮到大家吧,培养优质大数据打工人!——By Alexie-Z-Yevich 2022.6.22
这门课考试还真没为难大家,比较难的就最后一题需要计算,但是其实老师上课都已经讲过了并且在复习阶段都已经教过大家怎么去写。分值也不算太高,最后一个大题占16分,其余都是送分题,需要补充的东西并不多,基本上以这个文档内容来说完全足够了。——By Alexie-Z-Yevich 2022.7.1
