算法设计与分析

前置知识

vector

C++ STL中的verctor好比是C语言中的数组，但是vector又具有数组没有的一些高级功能。与数组相比，vector就是一个可以不用再初始化就必须制定大小的边长数组。

算法中常见的vector L(n, 0)表示生成一个L包含n个重复的元素，每个元素值为0。

set

set就是集合，STL的set用二叉树实现，集合中的每个元素只出现一次(参照数学中集合的互斥性)，并且是排好序的(默认按键值升序排列)

访问元素的时间复杂度是O(log2n) 。

queue

queue是一种容器转换器模板，调用#include< queue>即可使用队列类。在算法中通常是作为FIFO队列使用。

常见形式：queue<Type, Container> (<数据类型，容器类型>）

functional

类模板std::function是通用多态函数封装器。 std::function的实例能存储、复制及调用任何可调用函数、 lambda表达式、 bind表达式或其他函数对象，还有指向成员函数指针和指向数据成员指针。

简单来说就是在函数中实现内嵌函数，但是内嵌函数同样适用于递归，且可以获得外层函数的参数。

结构体

template<class T>
struct BtNode
{ 
    T data;
 	int depth = 1;
 	BtNode *left = 0, *right = 0;
};

结构体属于用户自定义的数据类型，允许用户存储不同的数据类型。写法如上述。

Matrix

矩阵运算库，在算法中以老师给的Matrix.hpp为准，建议浏览一下内容，知道诸如.row()函数、G(x,y)等运算都来源于自建库，附上我使用版本的Matrix.hpp：

// Matrix.hpp
#pragma once
#include<vector>
#include<iostream>
using namespace std;
template<class T>
class Matrix
{  
   vector<T> buf; // 用一维数组保存矩阵元素
   size_t r = 0, c = 0; // 行数和列数
public:
   Matrix() = default; // 默认初始化
   Matrix(const Matrix &m) = default; // 使用另一矩阵初始化
   ~Matrix() = default; // 析构
   Matrix &operator=(const Matrix &) = default; // 赋值
   Matrix(size_t row, size_t col): // 根据行数和列数初始化
      buf(vector<T>(row * col)), r(row), c(col) {}
   Matrix(size_t row, size_t col, const T &v): // 用行数和列数及指定值初始化
      buf(vector<T>(row * col, v)), r(row), c(col) {}
   // 使用初始值列表初始化, 即使用{}初始化
   Matrix(const initializer_list<initializer_list<T>> &m):
      buf(begin(m)->begin(), rbegin(m)->end()), // 指定元素
      r(m.size()), c(begin(m)->size()) // 指定行数和列数
   {}
   void assign(const T &v) // 每个元素都是v
   {  
      buf.assign(r * c, v);
   } // 耗时O(size)
   // 元素类型简写
   using reference = typename vector<T>::reference; // 元素引用
   using const_reference = typename vector<T>::const_reference; // const引用
   reference operator()(size_t i, size_t j) // 使用M(i, j)的形式访问矩阵元素
   {  
      return buf[i * c + j];
   }
   const_reference operator()(size_t i, size_t j) const
   {  
      return buf[i * c + j];
   }
   size_t rows() const { return r; } // 行数
   size_t cols() const { return c; } // 列数
   //
   // extend
   //
   Matrix(Matrix &&m): buf(move(m.buf)), r(m.r), c(m.c) {}
   Matrix &operator=(Matrix &&m)
   {  
      buf = move(m.buf), r = m.r, c = m.c;
      return *this;
   }
   Matrix &operator=(const initializer_list<T> &m)
   {  
      buf.assign(m);
      return *this;
   } // 使用列表赋值，即将{}中的元素复制到*this
   size_t size() const { return r * c; } // 元素数
   //
   // end extend
   //
};
//
template<class T> // 输出矩阵的所有元素
ostream &operator<<(ostream &out, const Matrix<T> &m)
{  
   size_t r = m.rows(), c = m.cols();
   for(size_t i = 0; i < r; ++i)
   {  
       for(size_t j = 0; j < c; ++j)
         out << m(i, j) << ' ';
      out << endl; // 输出一行元素后换行
   }
   return out;
} // 耗时O(size)
//
// extend
//
template<class T> // 两个矩阵相加
auto operator+(const Matrix<T> &X, const Matrix<T> &Y)
{  
   size_t r = min(X.rows(), Y.rows()), c = min(X.cols(), Y.cols());
   Matrix<T> Z(r, c);
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(i, j) + Y(i, j);
   return Z;
}
template<class T> // 两个矩阵相减
auto operator-(const Matrix<T> &X, const Matrix<T> &Y)
{  
   size_t r = min(X.rows(), Y.rows()), c = min(X.cols(), Y.cols());
   Matrix<T> Z(r, c);
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(i, j) - Y(i, j);
   return Z;
}
template<class T> // 两个矩阵相乘
auto operator*(const Matrix<T> &X, const Matrix<T> &Y)
{  
   size_t r = X.rows(), c = Y.cols(), m = min(X.cols(), Y.rows());
   Matrix<T> Z(r, c);
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
      {  
         Z(i, j) = X(i, 0) * Y(0, j);
         for(size_t k = 1; k < m; ++k)
            Z(i, j) = Z(i, j) + X(i, k) * Y(k, j);
      }
   return Z;
}
template<class T, class T2> // 加上一个值
auto operator+(const Matrix<T> &X, const T2 &v)
{  
   size_t r = X.rows(), c = X.cols();
   Matrix<T> Z(r, c); // 结果矩阵
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(i, j) + v;
   return Z;
}
template<class T, class T2> // 减去一个值
auto operator-(const Matrix<T> &X, const T2 &v)
{  
   size_t r = X.rows(), c = X.cols();
   Matrix<T> Z(r, c); // 结果矩阵
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(i, j) - v;
   return Z;
}
template<class T, class T2> // 乘以一个值
auto operator*(const Matrix<T> &X, const T2 &v)
{  
   size_t r = X.rows(), c = X.cols();
   Matrix<T> Z(r, c); // 结果矩阵
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(i, j) * v;
   return Z;
}
template<class T, class T2> // 除以一个值
auto operator/(const Matrix<T> &X, const T2 &v)
{  
   size_t r = X.rows(), c = X.cols();
   Matrix<T> Z(r, c); // 结果矩阵
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(i, j) / v;
   return Z;
}
template<class T> // 负
auto operator-(const Matrix<T> &X)
{  
   return X * (-1);
}
template<class T> // 转置
auto transpose(const Matrix<T> &X)
{  
   size_t r = X.cols(), c = X.rows();
   Matrix<T> Z(r, c);
   for(size_t i = 0; i < r; ++i)
      for(size_t j = 0; j < c; ++j)
         Z(i, j) = X(j, i);
   return Z;
}
//
// end extend
//

渐进符号

渐进符号O（上界）【考点】

1、符号O的定义

f(n) = O(g(n))当且仅当存在正整数c和n0，使得n >= n0时，有f(n) <= c * g(n)。此时，称g(n)是f(n)的一个上界。

常数函数	f(n) = C0 = O(1)	c = C0, n0 = 0
线性函数	3n + 2 = O(n)	c = 4, n0 = 2
线性函数	100n + 6lnn = O(n)	c = 102, n0 = 6
平方函数	10n ^ 2 + 4n + 3 = O(n ^ 2)	c = 11, n0 = 5
平方函数	nlogn + n ^ 2 = O(n ^ 2)	c = 2, n0 = 3
指数函数	6 x 2 ^ n + n ^ 2 = O(2 ^ n)	c = 7, n0 = 4
松散界限	3n + 2 = O(n ^ 2)	c = 3, n0 = 2
错误界限	3n + 2 ≠ O(1)

注意：

（1）不要产生松散界限；（2）不要产生错误界限；（3）f(n)与g(n)顺序不能调转。

2、【大O比率定理】

$$
对于函数f(n)和g(n)，如果\lim_{n\rightarrow + \infty}\frac{f(n)}{g(n)}存在，则f(n) = O(g(n))当且仅当c > 0,使得\lim_{n\rightarrow + \infty}\frac{f(n)}{g(n)} ≤ c。
$$

3、【常用上界关系定理】 (由大O比率定理证明)

$$
对于任何正数x和ε，
\log^{-x}n = O(1),
x = O(\log^{ε}n),
\log^{x}n = O(\log^{x + ε}n),
\log^{x}n = O(n^{ε}),\
n^x = O(n^{x + ε}),
n^x = O(2^n)和2^n = O(2!)
等上界关系都成立。
$$

总结：常用上界关系就是通常所说的向上约分，需要注意的是常用上界关系定理中的转换公式，理解与学会转换诸如：
$$
\log^{20}n = O(n^{1.5})
$$

渐进符号Ω（下界）

1、符号Ω的定义

f(n) = Ω(g(n))当且仅当存在正常数c和n0，使得当n ≥ n0时，有f(n) >= c * g(n)。

2、【大Ω比率定理】

$$
对于f(n)和g(n)，如果\lim_{n\rightarrow + \infty}\frac{g(n)}{f(n)}存在，则f(n) = Ω(g(n))当且仅当存在c > 0，使得\lim_{n\rightarrow + \infty}\frac{g(n)}{f(n)} <= c。
$$

渐进符号Θ（双界）

1、符号Θ的定义

f(n) = Θ(g(n))当且仅当存在正常数c1，c2和n0，使得当n >= n0时，有c1 * g(n) <= f(n) <= c2 * g(n)。

2、【大Θ比率定理】

$$
对于函数f(n)和g(n)，如果\lim_{n\rightarrow + \infty}\frac{f(n)}{g(n)}与\lim_{n\rightarrow + \infty}\frac{g(n)}{f(n)}都存在，则f(n) = Θ(g(n))当且仅当存在正常数c1，c2，\
使得\lim_{n\rightarrow + \infty}\frac{g(n)}{f(n)} <= c1, \lim_{n\rightarrow + \infty}\frac{f(n)}{g(n)} <= c2。
$$

• 大Θ比率定理是大O比率定理与大Ω比率定理的结合。

简化Master定理【考点】

1、定理适用范围

当a > 0, b > 1, α >= 0时，对于形如T(n) = aT(n / b) + X(n ^ α)（其中，X代表O、Ω、Θ之一，n / b可以理解为[n / b]【这里无法描述】）的递归函数，可以使用简化Master定理找到他们的渐进函数。

2、简化Master定理

$$
当a > 0, b > 1, α >= 0时，递归函数T(n) = aT(n / b) + X(n ^ α)(X代表O、Ω、Θ之一)的渐进函数为 \
T(n) =
\begin{cases}
X(n^{\log_ba}), α < \log_ba \
X(n^αlogn), α = \log_ba \
X(n^α), α > \log_ba
\end{cases}
$$

• 通过简化Master定理我们求的是Θ的渐进函数。

排序算法

选择排序（升序排列）

template<class T>
int Max(T X[], int n)
{ 
    int pos = 0;
 	for(int i = 1; i < n; ++i)
 		if(X[pos] < X[i]) pos = i;
 	return pos;  // 返回数组最大值的下标
}
template<class T>
void SelectionSort(T X[], int n)
{ 
    for(int m = n; m > 1; --m){ 
        int i = Max(X, m);  // 找到当前数组的最大值
 		swap(X[i], X[m - 1]);  // 将最大值与数组未遍历末位交换
	}
}
// 时间复杂度为O(n ^ 2)

插入排序（升序排列且不含重复元素）

// 将元素插入到有序数组中
template<class T, class T2>
int Insert(T X[], int m, const T2 &v)  // v为要插入的元素
{ 
    int p;
 	for(p = m - 1; p >= 0 and X[p] > v; --p) {}  // 用p记录第一个比v小的数组下标
 	if(X[p] == v) return m;  // 如果两数据相等，不执行插入操作
	for(int i = m - 1; i > p; --i)
 		X[i + 1] = X[i];  // 所有数据向后移一位
 	X[p + 1] = v;
 	return m + 1;
}
// 时间复杂度为O(m)

插入排序（升序排列）

// 将无序数组进行插入排序
template<class T>
void Insert(T X[], int m, const T &v)
{ 
	int i;
 	for(i = m - 1; i >= 0 and X[i] > v; --i)  // 找到第一个比传入元素小的下标，将其他元素向后移动
 		X[i + 1] = X[i];
 	X[i + 1] = v;
}
template<class T>
void InsertionSort(T X[], int n)
{ 
	for(int m = 1; m < n; ++m){ 
		auto v = X[m];
 		Insert(X, m, v);
 	}
}
// 时间复杂度为O(n ^ 2)

图遍历方法

一般树的先序遍历

template<class T>
struct BtNode
{ 
    T data;
 	BtNode *left = 0, *right = 0;
};
template<class T, class Func>
void PreOrder(BtNode<T> *x, Func Visit)
{ 
    if(x == 0) return;
 	Visit(x);
 	PreOrder(x->left, Visit);
 	PreOrder(x->right, Visit);
}

二叉树的层次遍历

template<class T>
struct BtNode
{ 
    T data;
 	BtNode *left = 0, *right = 0;
};
template<class T, class Func>
void LevelOrder(BtNode<T> *x, Func Visit)
{ 
    if(x == 0) return;
	queue<BtNode<T> *> Q;  // 创建队列（先入先出）
 	Visit(x), Q.push(x);
 	while(not Q.empty()){ 
        x = Q.front(), Q.pop();  // 取Q队列的第一个元素出队。
 		auto left = x->left, right = x->right;
 		if(left != 0)
 			Visit(left), Q.push(left);  // 将x左子树元素入队
 		if(right != 0)
 			Visit(right), Q.push(right);  // 将x右子树元素入队
 	}
}
// 其实类似先序遍历，都是先执行Visit操作后再进行左右子树判断；
// 主要区别在于层次遍历是一个入队出队操作，先判断队列中是否有元素，再去将元素的左右子树依次入队。

连通图的宽度优先搜索算法

template<class Fun>
void BFS(Matrix<bool> &G, int v, vector<bool> &Visited, Fun Visit)
{ 
    int n = G.rows();
 	queue<int> Q;
 	Visit(v), Visited[v] = 1, Q.push(v);  // Visit函数代表进行访问操作，数组Visited记录元素元素是否被访问
 	while(not Q.empty()){ 
        v = Q.front(), Q.pop();
 		for(int w = 0; w < n; ++w)
 			if(not Visited[w] and G(v, w) == 1)
 				Visit(w), Visited[w] = 1, Q.push(w);
 	}
}
// 和树的层次遍历一模一样，区别就是树一般为二叉树，只有两个子节点，但是图是每个节点都有可能相连；
// 所以在宽度搜索时是将没有访问过的一排节点（相连）全部入队。

连通图的深度优先算法

template<class Fun>
void DFS(Matrix<bool> &G, int v, vector<bool> &Visited, Fun Visit)
{ 
    int n = G.rows();
 	Visit(v), Visited[v] = 1;
 	for(int w = 0; w < n; ++w)
 		if(not Visited[w] and G(v, w) == 1)
 			DFS(G, w, Visited, Visit);  // 递归去寻找未访问的节点
}

二叉树的深度优先搜索（改）计算每个节点的深度

#include<algorithm>
template<class T>
struct BtNode
{ 
    T data;
 	int depth = 1;
 	BtNode *left = 0, *right = 0; // 左子树, 右子树
};
template<class T>  // 使用后根遍历的方法计算深度
int Depth(BtNode<T> *x)
{ 
    if(x == 0) return 0;
 	x->depth = std::max(Depth(x->left), Depth(x->right)) + 1;  // 递归向上回溯深度
 	return x->depth;
}

一般树的深度优先搜索（改）计算每个节点的层次

template<class T>
struct TreeNode
{ 
    T data;
 	int level = 1;
 	TreeNode *first = 0, *next = 0;  // first、next的作用类似于首位坐标
};
template<class T>  // 使用先根遍历的方法计算层次
void Level(TreeNode<T> *x, int level)
{ 
    if(x == 0) return;
 	x->level = level;  // 
 	for(auto w = x->first; w != 0; w = w->next)  // 这里就是层次遍历的体现，将first开始到最后一个next节点
 		Level(w, level + 1);
}

连通图的深度优先遍历算法（改）计算每个顶点的层次

#include "Matrix.hpp"  // 图计算的依赖
#include "ios.hpp"
    #include <functional>
auto Level(const Matrix<bool> &G, int u = 0)
{ 
    int n = G.rows();
 	vector<int> L(n, 0);  // 设置L中有n个元素，每个元素值为0
 	function<void(int, int)>
 	Level = [&](int u, int level){  // 区别于外面一圈Level函数，可以调用外圈Level中的参数
        L[u] = level;
 		for(int w = 0; w < n; ++w)
 			if(L[w] == 0 and G(u, w) == 1)
 				Level(w, level + 1);
 	};
 	Level(u, 1);
 	return L;
}

图的宽度优先遍历算法（改）输出图的每个连通分支

#include "../algorithm.h"
auto BFS(Matrix<bool> &G, int v, vector<bool> &Visited)
{ 
    int n = G.rows();
 	queue<int> Q;
 	set<int> part;
 	part << v, Visited[v] = 1, Q.push(v);
 	while(not Q.empty()){ 
        v = Q.front(), Q.pop();
 		for(int w = 0; w < n; ++w)
 			if(not Visited[w] and G(v, w) == 1)
 				part << w, Visited[w] = 1, Q.push(w);
 		}
 	return part;
}
auto BFT(Matrix<bool> &G)
{ 
    int n = G.rows();
 	vector<bool> Visited(n, 0);
 	vector<set<int>> parts;  // 创建一个动态大小的数组parts记录int集合
 	for(int v = 0; v < n; ++v)
 		if(not Visited[v])
 			parts << BFS(G, v, Visited);  // 将每个节点都遍历一遍
 	return parts;
}
// 和连通图的主要差别就是BFT函数将所有节点扫一遍，避免出现有些节点单出来的情况。
//[1,1,1,0,0],
//[1,1,1,0,0],
//[1,1,1,0,0],
//[0,0,0,1,1],
//[0,0,0,1,1]

分治方法

折半搜索（升序数组）

// 从一个升序数组中查找一个元素
template<class T, class T2>
int search(T X[], int n, const T2 &v)
{ 
   	int low = 0, up = n;
 	while(low < up){ 
        int m = (low + up) / 2;
 		if(v == X[m]) return m;
 		else if(v < X[m]) up = m;
 		else low = m + 1;
 	}
 	return -1;
}
// 时间复杂度为O(log(n))

归并排序

template<class T>
void Merge(T W[], int low, int m, int up)
{ 
    vector X(W + low, W + m);  // 创建动态数组X长度为low~m，存入low~m的数据
 	vector Y(W + m, W + up);  // 创建动态数组Y长度为m~up，存入m~up的数据
 	int nx = size(X), ny = size(Y);
 	int i = 0, j = 0, k = low;
 	while(i < nx and j < ny)  // 将X、Y中数据进行比较，存入W数组
 		if(X[i] < Y[j])
 			W[k] = X[i], ++k, ++i;
 		else
 			W[k] = Y[j], ++k, ++j;
 	while(i < nx)  // 将比较完后未存入的元素存入
 		W[k] = X[i], ++k, ++i;
 	while(j < ny)
 		W[k] = Y[j], ++k, ++j;
}
template<class T>
void MergeSort(T X[], int low, int up)
{ 
    if(up - low <= 1) return;
 	int m = (low + up) / 2;
 	MergeSort(X, low, m);  // 左右递归再向上排序
 	MergeSort(X, m, up);
 	Merge(X, low, m, up);
}
// 时间复杂度为Θ(n * log(n))

快速排序

template<class T>
int Partition(T X[], int low, int up)
{ 
    int key = up - 1, p = low;
 	for(int i = low; i < key; ++i)  // 每次将比最后一个数小的数排到数组的前面
 		if(X[i] < X[key])
 			swap(X[i], X[p]), ++p;
 	swap(X[key], X[p]);  // 如果前面所有数都比X[key]小，那么swap(X[key], X[p])实际为swap(X[key], X[key])
 	return p;
}
template<class T>
void QuickSort(T X[], int low, int up)
{ 
    if(up - low <= 1) return;
 	int m = Partition(X, low, up);
 	QuickSort(X, low, m);  // 不断缩小左右区间，直到完成排序
 	QuickSort(X, m + 1, up);
}
// 平均时间复杂度为O(n * log(n))，最坏时间复杂度为O(n ^ 2)

线性时间选择算法

template<class T>
int Partition(T X[], int low, int up)
{ 
    int key = up - 1, p = low;
 	for(int i = low; i < key; ++i)
 		if(X[i] < X[key])
 			swap(X[i], X[p]), ++p;
 	swap(X[key], X[p]);
 	return p;
}
template<class T>
T &Select(T X[], int n, int k)
{ 
    int low = 0, up = n;
 	for(;;){ 
        int m = Partition(X, low, up);
 		if(k == m) return X[m];  // 找到指定元素，算法终止
 		else if(k < m) up = m;
 		else low = m + 1;
 	}
}
// 平均时间复杂度为O(n)，最坏时间复杂度为O(n ^ 2)
// 显而易见，这里的Partition函数和上题的一模一样，因此最坏情况（数组降序）时时间复杂度为O(n ^ 2)
// 这个算法主要是用来在乱序数组中寻找指定元素

合并数组（不含重复元素）

template<class T>
int Merge(T X[], int m, T Y[], int n, T W[])
{ 
    int i = 0, j = 0, k = 0;
 	while(i < m and j < n)
 		if(X[i] < Y[j])
 			W[k] = X[i], ++k, ++i;
 		else if(X[i] > Y[j])
 			W[k] = Y[j], ++k, ++j;
 		else
 			W[k] = X[i], ++k, ++i, ++j;
 	while(i < m)
 		W[k] = X[i], ++k, ++i;
 	while(j < n)
 		W[k] = Y[j], ++k, ++j;
 	return k;
}
// 和归并排序的merge函数基本一模一样，就不做赘述

奇偶划分

int Partition(int X[], int n)
{ 
    int p = 0;
 	for(int i = 0; i < n; ++i)
 		if(X[i] % 2 == 1)
 			swap(X[i], X[p]), ++p;
 	return p;
}

贪心算法

装载问题

vector<bool> Load(vector<double> &W, double M)
{ 
    int n = W.size();
 	sort(begin(W), end(W));  // 从小到大排序
 	vector<bool> X(n, 0);
 	double rc = M;
 	for(int i = 0; i < n and W[i] <= rc; ++i)
 		X[i] = 1, rc -= W[i];
 	return X;
}

背包问题

void Sort(vector<double> &V, vector<double> &W)
{ 
    struct oType { double v, w; };  // 一个物品具有价值、重量两个属性
 	auto cmp = [](oType p, oType q){ 
        return p.v / p.w > q.v / q.w;
 	};
 	int n = min(V.size(), W.size());
 	vector<oType> X(n);
 	for(int i = 0; i < n; ++i)
 		X[i] = {V[i], W[i]};
 	sort(begin(X), end(X), cmp);  // 这个可能是按照cmp规则对X进行排序（题主C++不太好QWQ）
 	for(int i = 0; i < n; ++i)
 		V[i] = X[i].v, W[i] = X[i].w;
}
vector<double> Knap(vector<double> &V, vector<double> &W, double M)
{ 
    int n = min(V.size(), W.size());  // 避免出现价值、重量不同导致物品个数出问题
 	Sort(V, W);
 	vector<double> X(n, 0);
 	double rc = M;
 	int t;
 	for(t = 0; t < n and W[t] <= rc; ++t)
 		X[t] = 1, rc -= W[t];
 	if(t < n)  // 这一步很多余，毕竟不可能只把一个物品放一部分进背包
 		X[t] = rc / W[t];
 	return X;
}
// Knap函数在Sort函数下部分与装载问题无异，因此Sort函数主要是将价值/重量进行排序

活动安排问题

已知n个活动E = {1，2，…，n}需要使用同一资源，第k个活动的开始和结束时间分别是s_k和f_k，其中s_k < f_k, k = 1，2，…，n。

简单来说就是一个集合中有若干元素，每个元素含有起始（s_k）、结束（f_k）两个值，只有在起始时间才能开始，占用资源直到结束时间结束，经历了起始和结束的元素才能进入子集。求这个集合中能完成的最大子集。

贪心思想就是当一个活动结束立即找到一个活动开始，优先找到结束时间早的活动。

void Sort(vector<double> &S, vector<double> &F)
{ 
    struct oType { double s, f; };
 	auto cmp = [](oType p, oType q){ 
        return p.f < q.f;  // 按照结束时间进行排序
 	};
 	int n = min(S.size(), F.size());
 	vector<oType> X(n);
 	for(int i = 0; i < n; ++i)
 		X[i] = {S[i], F[i]};
 	sort(begin(X), end(X), cmp);
 	for(int i = 0; i < n; ++i)
 		S[i] = X[i].s, F[i] = X[i].f;
}
vector<bool> Action(vector<double> &S, vector<double> &F)  // S是起始时间数组；F是结束时间数组（Start/Final）
{ 
    int n = min(S.size(), F.size());
 	Sort(S, F);
 	vector<bool> X(n, 0);
 	X[0] = 1;
 	for(int i = 1, j = 0; i < n; ++i)
 		if(S[i] >= F[j])
 			X[i] = 1, j = i;
 	return X;
}
// 主体和背包问题类似，明确两者的贪心条件区别，可以同时记忆

最小生成树Prim算法

从图的任一节点开始，每次找到与该节点连通的最短路径的节点（未被访问），直到遍历完所有节点

// .assign()：C++ string类的成员函数，用于拷贝、赋值操作，它们允许我们顺次地把一个string 对象的部分内容拷贝到另一个string 对象上。
// isinf()函数是cmath标头的库函数，用于检查给定值是否为无限(负无穷大或正无穷大)。如果给定值是无穷大，则返回1；否则，返回0。 
bool Prim(const Matrix<double> &G, int v, vector<int> &prev)
{ 
    int n = G.rows();
 	prev.assign(n, v); // prev保存各节点的父亲，初始为根v（这里不写0是因为可能你设置的起始节点不是0）
 	vector<bool> S(n, false);  // 记录节点是否被选，初始值为false
 	S[v] = true;
 	for(int i = 0; i < n - 1; ++i){ 
        double min = INFINITY;
 		for(int w = 0; w < n; ++w)
 			if(not S[w] and G(prev[w], w) < min) 
                min = G(prev[w], w), v = w;  // 找到与节点相邻的最短边
 		if(isinf(min)) return false;  // 判断节点间是否连通
 		S[v] = true;
 		for(int w = 0; w < n; ++w)
 			if(not S[w] and G(v, w) < G(prev[w], w))  // 更新未选顶点的父亲）
                prev[w] = v;
 	}
 	return true;
}
// 该题主要用于判断无向图是否连通

最小生成树Kruskal算法

将节点之间的边按照升序排列，选取最短边，在不形成环的情况下遍历完所有节点。

bool Kruskal(vector<Edge> &Ed, int n, vector<Edge> &X)
{ 
    if(Ed.size() < n - 1) return false;  // 边数比节点个数少不可能连通
 	sort(begin(Ed), end(Ed));
 	UnionFind U(n);  // 并查集结构，初始将每个节点作为一个子树
 	X = {};
 	for(auto e : Ed){ 
        int u = U.Find(e.u), v = U.Find(e.v);
 		if(u == v) continue;  // 两节点是一个分支的，不用合并直接进入下一个节点判别
 		U.Union(u, v);
 		X.push_back(e);  // 记录节点e已被使用
 		if(X.size() >= n - 1) return true;
 	}
 	return false;
}	

多机调度问题

#include<queue.hpp>
using namespace std;
struct Machine { int i, tm; }; // 机器号, 使用时间
bool operator<(const Machine &x, const Machine &y)
{ 
    return x.tm < y.tm; // 比较使用时间
}
auto InitMachine(int m) // 初始化机器和最小堆
{ 
    minheap<Machine> H;
 	for(int i = 0; i < m; ++i)
 		H.push({i, 0});
 	return H;
}
auto LPT(vector<int> &J, int m) // n是作业数, m是机器数, n>m
{ 
    sort(begin(J), end(J)); // 作业按照所需处理时间升序排列
 	auto H = InitMachine(m); // 初始化机器和最小堆
 	int n = J.size(); // 作业数
 	vector<int> X(n); // 当前调度
 	for(int t = n - 1; t >= 0; --t) // 从处理时间最长的作业开始
 	{ 
        auto [i, tm] = H.top(); H.pop(); // 选用最早空闲的机器
 		X[t] = i, tm += J[t]; // 作业t安排到机器i
 		H.push({i, tm});
 	}
 	return X;
}
// 因为这题代码过长，强行理解不如按照自己的思路去写一个全新的，所以对于参考代码不做过多赘述。

多级调度问题主要是n个机器、m个作业，每个作业用时不等（可以相等），求最短调度时间。

整体思路（仅供参考）：

（1）将作业调度时间降序排列；（2）找到当前时间最短的机器插入作业；（3）判断下一个作业。

public int Solution(int n, int m, int T[]){
    int[] a = new int[n];  // 记录各机器调度时间
    Arrays.sort(T,Collections.reverseOrder());  // 降序排列
    for(int i = 0;i < m;i++){
        int min = INFINITY;
        int pom = 0;
        for(int j = 0;j < n;j++){
            if(a[j] < min){
                min = a[j];
                pom = j;  // 记录最短调度机器下标
            }
        }
        a[pom] += m;
    }
    int max = 0;
    for(int i = 0;i < n;i++){  // 找出所有机器中耗时最长的那个
        if(max < a[i])
            max = a[i];
    }
    return max;
}

动态规划算法

矩阵连乘最优次序

主要是n个矩阵进行矩阵乘法运算时，通过括号改变运算的先后顺序，减少运算次数，找到最佳划分方法，求解最少运算次数.

Matrix<int> MatrixChain(int r[], int n)
{ 
    Matrix<int> c(n, n, 0), kay(n, n);  // c(i, j)存储矩阵i连乘矩阵j中的最小值，kay记录分段位置
 	for(int i = n - 2; i >= 0; --i){  // 第一层循环从链末尾向前保存最优路径
        for(int j = i + 1; j < n; ++j){ 
            c(i, j) = (int)INFINITY;  // 初始连乘大小默认最大
 			for(int k = i; k < j; ++k){ 
                int t = c(i, k) + c(k + 1, j) + r[i] * r[k + 1] * r[j + 1];
 				if(t < c(i, j)) c(i, j) = t, kay(i, j) = k;
 			}
 		}
 	}
 	return kay;
}
// 时间复杂度为O(n ^ 3)
// 关于这题其实有些费解，因为矩阵能够连乘，因此可以近似看成一条链。具体我也说不很清，题主也是让别人教的QWQ

任意顶点间最短路径长度

Matrix< double> Floyd(const Matrix<double> &G)
{ 
    int n = G.rows();
 	auto A = G;
 	for(int k = 0; k < n; ++k)  // 第一层循环中的k作为中间节点
 		for(int i = 0; i < n; ++i)  // 二、三层分别为起始节点和终止节点
 			for(int j = 0; j < n; ++j){ 
                auto t = A(i, k) + A(k, j);  // 在这里将首尾相连，去除k
 				if(t < A(i, j)) 
                    A(i, j) = t;
 			}
 	return A;
}
// 时间复杂度为O(n ^ 3)
// 这个算法是直接将所有节点到任一节点的路径直接算出来了，如果要算任意节点可以直接找到结果

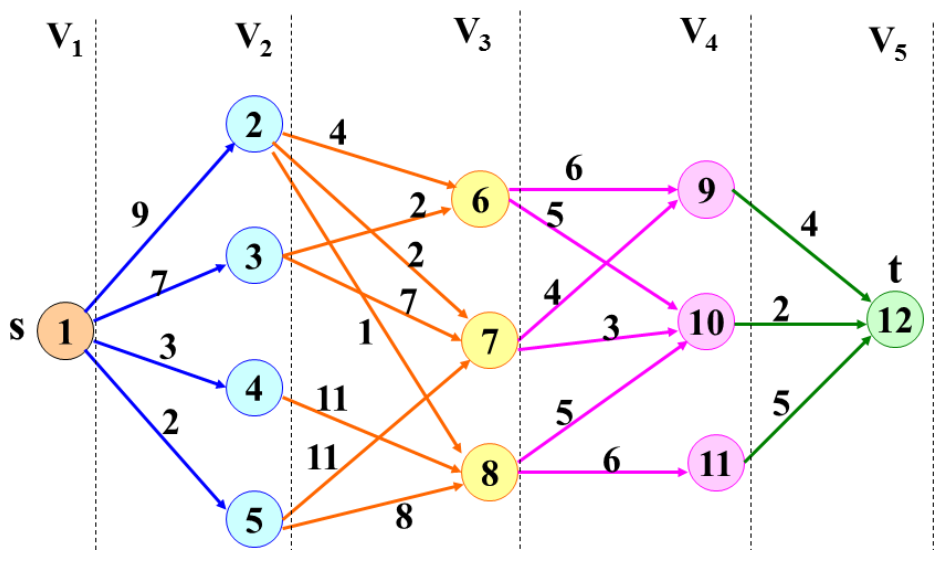
多段图

• 多段图是一个带权有向图并且无环
• 有且仅有一个起始点（原点source）和一个终止节点（汇点target）
• 它有n个阶段，每个阶段由特定的几个结点构成
• 每个结点的所有结点都只能指向下一个相邻的阶段，阶段之间不能越界(大概长这样)

vector<int> MultiGraph(const Matrix<double> &G, int m)
{ 
    int n = G.rows(), t = n - 1;  // n顶点数，t汇点（不包含起始点的中继点）
 	vector<double> C(n, 0);  // C[j]记录从初始节点到汇点的距离，初始为0
 	vector<int> Next(n);  // Next记录最短路径上所经过的后继节点
 	for(int j = t - 1; j >= 0; --j){  // 从终点向前计算
        int r = j + 1;
 		for(int i = r; i < n; ++i)
 			if(G(j, i) + C[i] < G(j, r) + C[r]) 
                r = i;
 		C[j] = G(j, r) + C[r], Next[j] = r;  // 存入当前节点到终点的最短路径，并且更新当前节点的后继节点
 	}
 	vector<int> X(m);
 	X[0] = 0;
 	for(int i = 1; i < m; ++i)  // 将后继节点转为从起点开始的正向顺序
 		X[i] = Next[X[i - 1]];
 	return X;
}
// 时间复杂度为O(n ^ 2)

两个字符串的最长公共子串

Matrix<int> LCSSize(const string &X, const string &Y)
{ 
    int m = X.size(), n = Y.size();
 	Matrix<int> C(m + 1, n + 1);  // 构建一个(m + 1, n + 1)大小的矩阵（从1开始，防止越界）
 	for(int i = 0; i <= m; ++i)
 		for(int j = 0; j <= n; ++j)
 			if(i <= 0 or j <= 0)
 				C(i, j) = 0;
 			else if(X[i - 1] == Y[j - 1])
 				C(i, j) = C(i - 1, j - 1) + 1;  // 计数代表公共子串有几个元素
 			else
 				C(i, j) = max(C(i - 1, j), C(i, j - 1));  // 从当前位置的上方或者左边选取较大值填充不相等区域
 	return C;
}
string LCS(const string &X, const string &Y)
{ 
    auto C = LCSSize(X, Y);
 	int i = X.size(), j = Y.size(), k = C(i, j);  // k代表最长子串元素个数
 	string Z;
 	while(k > 0)
 		if(X[i - 1] == Y[j - 1])  // 相等，矩阵脱最外层
 			Z.push_back(X[i - 1]), --i, --j, --k;
 		else if(C(i, j) == C(i - 1, j)) --i;
 		else --j;
 	reverse(begin(Z), end(Z));  // 反转
 	return Z;
}
// 时间复杂度为O(mn)，其中m=|X|, n=|Y|

0/1背包问题

一共有N件物品，每件物品都有其相应的体积和价值，给你一个背包，背包有容量上限，怎样往背包中装物品，能让背包中的物品价值最高。

#include<vector>
#include<map>
#include<functional>
using namespace std;
typedef vector<map<double, double>> RestType;  // 剩余表, 剩余容量-最优效益对数组
auto Knap(vector<double> &V, vector<double> &W, double c)  // 效益数组, 重量数组, 容量
{
 	int n = min(V.size(), W.size()); // 物品数
 	RestType M(n); // 剩余容量-最优效益对数组
 	function<double(int, double)> m = [&](int i, double y){ 
        if(M[i].count(y) > 0) 
            return M[i][y]; // 已经计算过, 返回
 		double cv; // 否则, 开始递归计算
 		if(i >= n - 1 and W[i] > y) 
            cv = 0;
 		else if(i >= n - 1) 
            cv = V[i];
 		else if(W[i] > y) 
            cv = m(i + 1, y);
 		else 
            cv = max(m(i + 1, y), m(i + 1, y - W[i]) + V[i]);
 		M[i][y] = cv;
 		return M[i][y];
 	};  // 调用m(0, c)耗时O(n^2 * 2^n)
 	auto fv = m(0, c);
 	return M;
}

题主表示比较嫌弃这种写法，和众所周知的AcWing上的解法差别还挺大的，因为这只是整体算法的一部分，理解起来反而很困难，但是如果要你把整个算法全部写出来，这样的写法一定非常鸡肋，所以下面是题主的代码，其实是取巧了，不像如上代码一样具有普适性，但是胜在容易理解和比较好写（对我来说）

public int Solution(int v[], int w[], int c){  // 效益数组, 重量数组, 容量
    int n = Math.max(v.length, w.length);  // 物品数
    int[][] dp = new int[n + 1][c + 1];  // dp记录背包内选择后的最大价值
    for(int i = 1;i <= n;i++){  // 枚举所有背包占用的情况
        for(int j = 0; j <= c;j++){
            if(j - w[i] >=0)
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[j]] + v[i]);  // 将第i件物品放入背包的效益与不放入背包的效益进行比较，决定第i件物品是否放入背包。
            else
                dp[i][j] = dp[i - 1][j];
        }
    }
    return dp[n][max];
}
// 这样子只能输出背包最大效益，如果想要知道选取的是哪些元素的话，要么还是参照老师的那种写法，要么在此写法上加上一段回溯。

写在前面：在上这门课之前题主没有接触过后面三个算法，因此基本上对来源什么的都不是很懂，大概估计后面三章会在回溯和剪枝出一道大题、概率出一道大题，一共两道大题20分。题主的建议是直接背吧，如果有兴致会在之后出一张本学年的押题卷，模仿样卷的题型罢了。

回溯方法

使用递归方法生成含 n 个分量的所有排列

求一个数组的全排列。举个例子方便大家理解：有数组[1,2,3]

全排列为[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]。

// iota函数用于对范围赋值
void B_Perm(int n)
{ 
    vector<int> X(n);
 	function<void(int)> Perm = [&](int t){ 
        if(t >= n) cout << X << endl;
 		else
 			for(int i = t; i < n; ++i){ 
                swap(X[t], X[i]);  // 交换两个数位置
 				Perm(t + 1);  // 交换下一个数（下一层）
 				swap(X[t], X[i]);  // 保持原数组不变
 			}
 	};
 	iota(begin(X), end(X), 0);  // 将X数组置为有序排列（例如X长度为3，则iota后X = [1,2,3]）
 	Perm(0);
}

使用递归方法生成 n 个元素的所有子集

求一个数组的所有子集。举个例子方便大家理解：有数组[1,2,3]

子集为{}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}。

void B_SubSet(int n)
{ 
    vector<bool> X(n);
 	function<void(int)> SubSet = [&](int t){
		if(t >= n) cout << X << endl;
 		else{
			X[t] = 1;  // 对X[t]元素进行判断，=1就是取，=0就是不取
 			SubSet(t + 1);  // 为两种状况分别构建队列
 			X[t] = 0;
 			SubSet(t + 1);
 		}
 	};
 	SubSet(0);
}

旅行商问题

// 旅行商问题可以看成是全排列问题，因为一定存在回路（不存在的边给了个INFINITY），所以只需要将所有节点的排列方式找出来，最短的就是最优路径。
vector<int> TSP(const Matrix<double> &G)
{ 
    int n = G.rows();
 	vector<int> X(n), BX;  // X存到当前节点的路径；BX存最优路径
 	double BC = INFINITY;  // 预设最大耗费
 	function<void(int, double)> TSP = [&](int t, double C){
        if(t >= n and C + G(X[n - 1], 0) < BC)  // 所有节点都到达且花费更少（答案更优）
 			BC = C + G(X[n - 1], 0), BX = X;
 		else if(t < n)
 			for(int i = t; i < n; ++i){
                swap(X[t], X[i]);
 				if(C + G(X[t - 1], X[t]) < BC)  // 如果当前路径比最优短，就接着找，已经超了也就没有找下去的必要了
 					TSP(t + 1, C + G(X[t - 1], X[t]));
 				swap(X[t], X[i]);
 			}
 	};
 	iota(begin(X), end(X), 0);  // 初始化
 	TSP(1, 0);  // 从第一站开始考虑，当前耗费为0
 	return BX;
}

子集和问题（36输出一个/不满足 & 38输出所有）

简单理解为给定一个数组W，给定一个数字M，求是否W存在子集的子集和等于M。

// 从题干就知道这一题类似于子集问题
vector<bool> SetSum(const vector<int> &W, int M)
{ 
    int n = W.size();
 	vector<bool> X(n), Y;
 	function<void(int, int, int)> SetSum = [&](int t, int s, int r){ 
        if(not Y.empty()) return;  // 不存在，结束
 		if(s == M) Y = X, Y.resize(t);
 		else if(t < n){
            X[t] = 1;
 			if(s + W[t] <= M)  // 每个元素依然是选或不选两种状态（选了之后仍然小于等于数字M）
                SetSum(t + 1, s + W[t], r - W[t]);
 			X[t] = 0;
 			if(s + (r - W[t]) >= M)  // 不选的话也要保证可选值大于等于数字M
                SetSum(t + 1, s, r - W[t]);
 		}
 	};
 	int s = 0, r = accumulate(begin(W), end(W), 0);  // accumulate求和函数，初始为0，累加X数组
 	SetSum(0, s, r);
 	return Y;
}

void SetSum(const vector<int> &W, int M)
{ 
    int n = W.size();
 	vector<bool> X(n);
 	function<void(int, int, int)> SetSum = [&](int t, int s, int r){ 
        if(s == M) cout << to_string(X, t) << endl;  // 存在一种情况直接输出
 		else if(t < n){
            X[t] = 1;
 			if(s + W[t] <= M) 
                SetSum(t + 1, s + W[t], r - W[t]);
 			X[t] = 0;
 			if(s + (r - W[t]) >= M) 
                SetSum(t + 1, s, r - W[t]);
 		}
 	};
 	int s = 0, r = accumulate(begin(W), end(W), 0);
 	SetSum(0, s, r);
}
// 显而易见，这两个代码块的区别在于Y，以及方法体中if-else中的if部分。优先记第二种，实在不行你把第二种写上老师都不会扣很多分。

最大团问题

求一个图中连通节点最多的子图

• 扫每一个节点，如果和团中所有节点都连通，可以存；
• 每个节点都有存和不存两种状态。

bool Connected(const Matrix<bool> &G, const vector<bool> &X, int t)  // 检查团与节点t的连接性
{ 
    for(int u = 0; u < t; ++u)
 		if(X[u] == 1 and G(t, u) == 0)  // 如果节点在当前团中但是没有与当前没有连接
            return false;
 	return true;
}
vector<bool> Clique(const Matrix<bool> &G)
{ 
    int n = G.rows(), fn = -1;  // fn记录最大团的顶点数
 	vector<bool> X(n), BX;  // X记录当前团，BX记录最大团
 	function<void(int, int)> Clique = [&](int t, int cn){ 
        if(t >= n and cn > fn) fn = cn, BX = X;
 		else if(t < n){ 
            X[t] = 1;
 			if(Connected(G, X, t)) Clique(t + 1, cn + 1);
 			X[t] = 0;
 			if(cn + n - (t + 1) > fn) Clique(t + 1, cn);
 		}
 	};
 	Clique(0, 0);
 	return BX;
}

着色问题

这个算是回溯中最难的一个了，依旧是前面的模板，但是写法稍有不同：

• 判断颜色是否和邻边相同，相同就给下一个节点变色，不同则检查下一个节点。

#include <vector>
#include <functional>
#include <Matrix.hpp>
using namespace std;
bool legal(const Matrix<bool> &G, vector<int> &X, int t)
{ 
    for(int i = 0; i < t; ++i)
 		if(G(i, t) == 1 and X[i] == X[t])  // 连通并且颜色相同返回false
            return false;
 	return true;
}
auto Chromatic(Matrix<bool> &G)
{ 
    int n = G.rows(), fm = n + 1; // 顶点数, fm最优颜色数（其实取n就够了，这里应该是为了让结果更加明显，便于debug）
 	vector<int> X(n), BX; // 当前方案, 最优方案
 	function<void(int, int)> Chromatic = [&](int t, int m){ // 搜索解空间树
 		if(t >= n and m < fm) // 答案(颜色数更小)
 			BX = X, fm = m;
 		else if(t < n)
 			for(X[t] = 1; X[t] <= m; ++X[t]){ 
                auto cm = max(X[t] + 1, m);  // 新的颜色数(可能需要增加)
 				if(legal(G, X, t) and cm < fm)  // X[t]可用且颜色数可能更小
 					Chromatic(t + 1, cm);  // 下一顶点
 			}
 		};
 	Chromatic(0, 1);  // 从顶点0开始, 初始颜色数为1, 上限为n
 	return BX;
}

分枝限界方法

通俗来说就是回溯算法中的剪枝操作，上面的回溯算法用的是深度优先遍历，那么下文的分枝限界算法就是用的宽度优先遍历，个人结论就是和图遍历一样，回溯用递归能解决，剪枝就需要用到队列queue了，如果还不是很懂queue的建议取找个文档简单阅读一下queue的基本操作。

使用分枝限界方法生成含 n 个分量的所有排列

• 首先我们明确一点就是回溯的思想是递归，而分枝限界的思想是递推，也就是说用通项公式来解决问题。

struct PermNode
{ 
    vector<int> X;
 	int t;
};
void Perm(int n)
{ 
    queue<PermNode> Q;
 	vector<int> X(n);  // X用来存数组中的元素排序，t用来存数组中的元素个数
 	iota(begin(X), end(X), 0);
 	Q.push({X, 0});
 	while(not Q.empty()){ 
        auto [X, t] = Q.front(); Q.pop();
 		if(t >= n) cout << X << endl;
 		else 
            for(int i = t; i < n; ++i)
 				swap(X[t], X[i]), Q.push({X, t + 1});  // 将所有的邻边全部入队
 	}
}

使用分枝限界方法生成 n 个元素的所有子集

struct SetNode
{ 
    vector<bool> X;
 	int t;
};
void SubSet(int n)
{ 
    queue<SetNode> Q;
 	vector<bool> X(n);
 	Q.push({X, 0});
 	while(not Q.empty()){ 
        auto[X, t] = Q.front(); Q.pop();
 		if(t >= n) cout << X << endl;
 		else{ 
            X[t] = 1, Q.push({X, t + 1});  // 为选了X[t]的元素构建一条队列
 			X[t] = 0, Q.push({X, t + 1});  // 为不选X[t]的元素构建一条队列
 		}
 	}
}

有了以上基础，以下三个就是大同小异了，这里不做过多解释。写不出来的话用前两题的思想套入问题，写写白话吧，毕竟这里不推荐大家背书。。。

旅行商问题

struct TSPNode
{ 
    vector<int> X;
 	int t;
 	double C;
};
bool operator<(const TSPNode &X, const TSPNode &Y)
{ 
    return X.C < Y.C;
}
vector<int> TSP(const Matrix<double> &G)
{ 
    minheap<TSPNode> H;
 	int n = G.rows();
 	vector<int> X(n), BX;
 	iota(begin(X), end(X), 0);
 	double C = 0, BC = INFINITY;
 	H.push({X, 1, C});
 	while(not H.empty()){ 
        auto [X, t, C] = H.top(); H.pop();
 		if(t >= n and C + G(X[n - 1], 0) < BC)
 			BC = C + G(X[n - 1], 0), BX = X;
 		else if(t < n)
 			for(int i = t; i < n; ++i){ 
                swap(X[t], X[i]);
 				if(C + G(X[t - 1], X[t]) < BC)
 					H.push({X, t + 1, C + G(X[t - 1], X[t])});
 			}
 	}
 	return BX;
}

最大团问题

bool Connected(const Matrix<bool> &G, const vector<bool> &X, int t)
{ 
    for(int u = 0; u < t; ++u)
 		if(X[u] == 1 and G(t, u) == 0) return false;
 	return true;
}
struct CliqueNode
{ 
    vector<bool> X;
 	int t, cn;
};
bool operator<(const CliqueNode &X, const CliqueNode &Y)
{ 
    return X.cn < Y.cn;
}
vector< bool> Clique(const Matrix<bool> &G)
{ 
    maxheap<CliqueNode> H;
 	int n = G.rows();
 	vector<bool> X(n), BX;
 	int cn = 0, fn = 0;
 	H.push({X, 0, cn});
 	while(not H.empty()){ 
        auto [X, t, cn] = H.top(); H.pop();
 		if(t >= n and cn > fn) fn = cn, BX = X;
 		else if(t < n){ 
            X[t] = 1;
 			if(Connected(G, X, t)) H.push({X, t + 1, cn + 1});
 			X[t] = 0;
 			if(cn + n - (t + 1) > fn) H.push({X, t + 1, cn});
 		}
 	}
 	return BX;
}

子集和问题（44输出所有 & 45输出一个/不满足）

struct SetSumNode
{ 
    vector<bool> X;
 	int t, s, r;
};
void SetSum(const vector<int> &W, int M)
{ 
    queue<SetSumNode> Q;
 	int n = W.size();
 	vector<bool> X(n);
 	int s = 0, r = accumulate(begin(W), end(W), 0);
 	Q.push({X, 0, s, r});
 	while(not Q.empty()){ 
        auto [X, t, s, r] = Q.front(); Q.pop();
 		if(s == M) cout << to_string(X, t) << endl;
 		else if(t < n){ 
            X[t] = 1;
 			if(s + W[t] <= M)
 				Q.push({X, t + 1, s + W[t], r - W[t]});
 			X[t] = 0;
 			if(s + (r - W[t]) >= M)
 				Q.push({X, t + 1, s, r - W[t]});
 		}
 	};
}

struct SetSumNode
{ 
    vector<bool> X;
 	int t, s, r;
};
vector<bool> SetSum(const vector<int> &W, int M)
{ 
    queue<SetSumNode> Q;
 	int n = W.size();
 	vector<bool> X(n), Y;
 	int s = 0, r = accumulate(begin(W), end(W), 0);
 	Q.push({X, 0, s, r});
 	while(not Q.empty()){ 
        if(not Y.empty()) break;
 			auto [X, t, s, r] = Q.front(); Q.pop();
 		if(s == M) Y = X, Y.resize(t);
 		else if(t < n){ 
            X[t] = 1;
 			if(s + W[t] <= M) Q.push({X, t + 1, s + W[t], r - W[t]});
 			X[t] = 0;
 			if(s + (r - W[t]) >= M) Q.push({X, t + 1, s, r - W[t]});
 		}
 	}
 	return Y;
}

概率方法

随机方法改写快速排序程序

template<class T>
int Partition(T X[], int low, int up)
{ 
    int key = rand() % (up - low) + low, p = low;  // key值随机生成，其他和快速排序一模一样
 	swap(X[key], X[up - 1]), key = up - 1;
 	for(int i = low; i < key; ++i)
 		if(X[i] < X[key]) 
            swap(X[i], X[p]), ++p;
 	swap(X[key], X[p]);
 	return p;
}
template<class T>
void QuickSort(T X[], int low, int up)
{ 
    if(up - low <= 1) return;
 	int m = Partition(X, low, up);
 	QuickSort(X, low, m);
 	QuickSort(X, m + 1, up);
}

随机方法改写基于划分的选择程序

template<class T>
int Partition(T X[], int low, int up)
{ 
    int key = rand() % (up - low) + low, p = low;  // key值随机生成，其他和选择排序一模一样
 	swap(X[key], X[up - 1]), key = up - 1;
 	for(int i = low; i < key; ++i)
 		if(X[i] < X[key]) 
            swap(X[i], X[p]), ++p;
 	swap(X[key], X[p]);
 	return p;
}
template<class T>
T &Select(T X[], int n, int k)
{ 
    int low = 0, up = n;
 	for(;;){ 
        int m = Partition(X, low, up);
 		if(k == m) return X[m];
 		else if(k < m) up = m;
 		else low = m + 1;
 	}
}

随机洗牌算法

template<class T>
void Shuffle(T X[], int n)
{ 
    for(--n; n > 0; --n)
 		swap(X[n], X[rand() % n]);  // 随机交换元素，将数组完全打乱
}

插入说明：

虽然题库里都是拉斯维加斯算法的求解过程，但是生活处处充满惊喜，谁也不知道他会不会出一个算法以外的题或者其他算法的题给你，因此在这里题主详细但又简洁的介绍下三种概率方法（蒙特卡洛算法、拉斯维加斯算法、舍伍德算法）

• 拉斯维加斯算法：不会得到错误解，但是有可能找不到解。（在下面的题目中形容得比较简单，对于需要排序的问题就是在开始将数组随机打乱；而对于需要求子集的问题，就是在判断一个元素选还是不选时引入随机数，就这么看来，概率算法其实是试卷的送分题【基础题型加一句随机数描述】）
• 蒙特卡洛算法：用于求问题的准确解，但是这个解不能保证是正确的。
• 舍伍德算法：总能得到问题的一个解，且得到的解一定是正确的。（通过确定算法引入随机数，消除/减少好坏实例之间的区别）

了解了这三个随机算法的区别后，考试的时候怎么办？如果真的出现了其他的概率算法怎么写？题主的建议是全按照拉斯维加斯算法的过程写，因为都是在基础题型上加上随机判断，三个算法的区别就是随机算法安插的位置和次数（1~2次）不同，所以没必要纠结之间的差别，拿个大头就好！

拉斯维加斯算法求解旅行商问题（是否存在耗费不超过t的旅行）

bool TSP(const Matrix<double> &G, double t, vector<int> &X)
{ 
    int n = G.rows();
 	iota(begin(X), end(X), 0);
 	random_shuffle(begin(X), end(X));  // 对一个数组随机排列
 	double s = 0;
 	for(int k = 0; k < n; ++k){ 
        s += G(X[k % n], X[(k + 1) % n]);
 		if(s > t) return false;
 	}
 	return true;
}

拉斯维加斯算法求解0/1背包问题（是否存在效益和不少于t的装包方式）

bool Knap(const vector<double> &V, const vector<double> &W,
double c, double t, vector<bool> &X)
{ 
    int n = min(V.size(), W.size());
 	double fv = 0, fw = 0;
 	for(int i = 0; i < n; ++i){ 
        if(rand() % 2 == 1)
 			X[i] = 1, fv += V[i], fw += W[i];
 		else
 			X[i] = 0;
 		if(fw > c) return false;
 	}
 	return fv >= t;
}

拉斯维加斯算法求解Hamilton回路问题（是否有Hamilton回路）

bool Hamilton(const Matrix<bool> &G, vector<int> &X)
{ 
    int n = G.rows();
 	iota(begin(X), end(X), 0);
 	random_shuffle(begin(X), end(X));
 	for(int k = 0; k < n; ++k){ 
        int i = X[k], j = X[(k + 1) % n];
 		if(G(i, j) != 1) return false;
 	}
 	return true;
}

拉斯维加斯算法求解子集和问题（是否存在和为t的子集）

bool SetSum(const vector<int> &W, int t, vector<bool> &X)
{ 
    int s = 0;
 	for(int i = 0; i < W.size(); ++i){ 
        if(rand() % 2 == 1)
 			X[i] = 1, s += W[i];
 		else
 			X[i] = 0;
 		if(s > t) return false;
 	}
 	return s == t;
}

拉斯维加斯算法求解团问题（是否存在顶点数不小于k的团）

bool Clique(const Matrix<bool> &G, int k, vector<bool> &X)
{ 
    int n = G.rows(), m = 0;
 	for(int i = 0; i < n; ++i)
 		if(rand() % 2 == 1)
 			X[i] = 1, ++m;
 		else
 			X[i] = 0;
 		if(m < k) return false;
 	for(int i = 0; i < n; ++i)
 		for(int j = i + 1; j < n; ++j)
 			if(X[i] == 1 and X[j] == 1 and G(i, j) != 1) return false;
 	return true;
}

总结

到这里，这门课这本书的所有内容（其实就是简单讲解了下题库）都已经完结了！恭喜恭喜，如果你是从头到尾认真一路复习下来的，那么毫无疑问，你八成已经忘得差不多了QWQ（因为题主两天半写到这发现真要随机抽一道给我确实不一定会写）。但是不用担心，基本上认真看到这的对于各问题的基本思路都已经成型，大家大可按照自己喜欢的、方便的语言去完成算法。两章回溯由于题主也是第一次接触，并且老师上课节奏较快（咱也不是认真听课的人），所以采用的是强记的方式。这两天题主会根据样卷出一份考前押题卷，一个是加强自己的手写能力，二个题库的题过了一遍，发现有些题太简单了，而有些题太难了，可以很大程度的缩小背记范围。那么，这个文档到此就告一段落了，之后应该是上传到GitHub上供未来的学弟学妹参考了（毕竟考前两天才完成）。

加油加油！ ——By Alexie-Z-Yevich 2022.5.8

---

算是版本2.0吧，因为之前对于回溯和分枝限界不是很了解，所以连带着概率也没怎么给大家写，今天把之前埋的坑都填上了，还是好难啊，押题卷昨天就出完了，大家感兴趣还是可以看一下滴。（其实今天又过了一遍题，如果真在题库里抽的话，那么其实没啥好押题的，真是谁也说不清呢） ——By Alexie-Z-Yevich 2022.5.9